How to Add Options Probabilities

Forums › ProRealTime English forum › General trading discussions › How to Add Options Probabilities

Viewing 15 posts - 1 through 15 (of 52 total)
1 2 3 4
  • 10/29/2021 at 6:30 PM #180571
    Bard

    Hi there, I was hoping a math expert here could tell me if it’s possible to add two probabilities when the probabilities are dependent? I assume they are from the way the Black Scholes option formula prices Calls and Puts, — where the value of the Call option (its premium) will go up (if the market rises and volatility changes) whilst the value of the Put option will go down)?

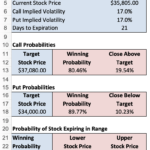
    What I have downloaded is an Excel Options probability calculator — pls see screenshot and Excel attachment. I don’t or can’t get the last table to do anything and don’t think it works?

    The Dow Jones price ranges (option Strikes) represent going short to open a Call (bearish, with the higher Strike, Dow 37,080) and going short to open a Put (bullish, with the lower Strike, Dow 34,000).

    The Short Strangle’s strategy objective is for the Dow to stay within the higher and lower Strike ranges (think of a dog with a vet cone around its head but in reverse!) and for the options to expire worthless (so you can close the trade out and buy the options back for less or zero and profit in the difference between the total premiums for the short Call and Put and the final contract (or earlier) option buy (closing) price.

    So is it possible (or wise) to add the two event probabilities and get a final total probability, which I think the last table in the Excel calculator was supposed to produce?

    Cheers, for any thoughts or input,

    Best,
    Bard

    10/29/2021 at 8:02 PM #180575
    JS

    The probability that the price will end up above the current share price of $35,805.00 is 50%.

    The probability that the price will end up below  the current share price of $35,805.00 is 50%

     

    The probability that the price will remain below  $ 37,080 is 80.46%

    The probability that the price will stay above  $ 34,000 is 89.77%

     

    The combined probability is then: 0.5 * 0.8046 + 0.5 * 0.8977 = 0.85115 (85.115 %)

    10/30/2021 at 9:25 AM #180587
    JS

    Buy Call (Long Call) = Bullish

    Sell Call (Short Call) = Bearish

     

    Buy Put (Long Put) = Bearish

    Sell Put (Short Put) = Bullish

     

    The maximum profit with a short strangle is fixed, namely the yield of the premiums of the short call and short put.

    The maximum loss (risk) is in principle unlimited.

     

    The probability that the price will remain between 34000 and 37080 before the expiration date is here: 85%

    10/30/2021 at 4:51 PM #180610
    Bard

    Hi JS,

    Thanks for taking the time to take a look at this and for your explanations. I have been reading how probabilities are multiplied not added for dependent events? https://www.investopedia.com/terms/a/additionruleforprobabilities.asp

    Also I was reading a Seeking Alpha article about Strangles:
    https://seekingalpha.com/article/4356459-what-to-watch-out-for-in-high-probability-strategies

    and they wrote:-
    “Theoretically speaking a 1 SD (std dev) short strangle with 45 days to expiration should have a probability of success of 68% (100 – 2 x 16%).”

    I guess the real question is how to mathematically define any Strangle trading range in terms of the probability distribution so that it gives 1, 2 and 3 Standard Deviations probabilities?

    Can a re-working of the Black Scholes formula provide that?
    https://www.investopedia.com/terms/b/blackscholes.asp

    ​

    1 user thanked author for this post.
    avatar PeterSt
    10/30/2021 at 5:07 PM #180611
    Bard

    Some points on Standard Deviations and the Probability Distribution:

    “Standard deviation measures certain outcomes relative to the average outcome. Here are how probabilities associated with certain multiples of standard deviations:
    One standard deviation encompasses approximately 68.2% of outcomes in a distribution of occurrences.

    Two does it for 95.4% and Three does 99.7%

    For example, if a £100 stock is trading with a 20% IV (implied volatility), the standard deviation ranges are:

    – One standard deviation – £80 to £120
    – Two standard deviations – £60 to £140
    – Three standard deviations – £40 to £160

    So what is the chances of that £100 stock staying between £80 and £120? 68.2%
    So what is the chances of that £100 stock staying between £60 and £140? 95.4%”

    https://unofficed.com/topic/risk-metrics-of-option-strangle/

    10/30/2021 at 10:43 PM #180625
    JS

    It is complicated because there are three cases:

     

    1. The price ends below OR above the current index price. The price can never end up both above and below the current index price at the same time, so this is a mutually exclusive event (you can add up the probabilities).
    2. The price ends below the current index price AND it drops to a certain limit, so this is a case where the events depend on each other (dependent events, here you have to multiply the probabilities with each other)
    3. The price ends above the current index price AND it rises to a certain limit, so this is also a case where the events depend on each other (the price must rise AND the price must rise to a certain limit). So again a dependent event where you have to multiply the probabilities with each other.

     

    So you have a 50% chance that the price will end up below the current index price and a 50% chance that the price will end up above the current index price. (indepent events)

     

    When the price falls (50% probability) AND it is allowed to fall to a certain value (89.77% chance) then the combined probability is 50% x 89.77% = 44.88% (dependent events).

    The chance is therefore 44.88% that the price will fall AND that the price will fall to the maximum of $ 34,000.

     

    When the price rises (50% probability) AND it is allowed to rise to the limit of $ 37,080 (80.46% chance) then the combined probability is 50% x 80.46% = 40.23% (dependent events). The chance is therefore 40.23% that the price will rise AND that the price will rise to the maximum of $ 37,080.

     

    Because the Short Strangle benefits from both an increase to a certain limit and a decrease to a certain limit (indepent events) you can add these probabilities together 44.88% + 40.23% = 85.11%

    So there is an 85.11% chance that the price will end up between the limits of $34,000 and $37,080.

     

     

    The standard deviation can (confusingly) refer to two concepts, namely the statistics of the numbers or the probability of these numbers.

    In statistics, the standard deviation is the degree of dispersion in certain data and indicates how far the data deviates from the average.

    In probability theory, the standard deviation is the probability of the deviation of the data from the mean. For example, if ±1 standard deviation from the average, 68.2% of the data will fall within these limits (with a normal distribution).

     

    So you have the volatility of the price and you have the probability that this (volatile) price remains within certain limits.

     

     

    With the Black & Scholes formula you can calculate the theoretical call and put option prices.

    The formula is so special because it can calculate prices of options that expire in the FUTURE, based on, among other things, volatility and the assumption that prices are normally distributed (random).

     

    If you want to calculate a short strangle in terms of probability then I do not know a ready-made solution (calculation help) for that but when you have access to the prices and data of options then you can look at the delta.

    The delta is the standard deviation of the options with also two values.

    The delta shows the degree of price change of an option.

    The delta also indicates the probability that the option will go into the money, a delta of 0.20 indicates that the option has a 20% chance of getting into the money (or getting to the target price). In terms of a short strangle, this option has an 80% chance of not getting to the target price.

    So if you want a short strangle with a probability of 68% then you have to sell options with a delta of 0.32 (1 – 0.68) and if you want a probability of 95% then you have to sell options with a delta of 0.05 (1 – 0.95).

    I hope it is clear… 🙂

    2 users thanked author for this post.
    avatar Bard, avatar PeterSt
    10/31/2021 at 10:40 AM #180638
    JS

    I have created a spreadsheet in Excel with which you can calculate the reliability interval based on:

    1. current rate (S)
    2. average annual return (m)
    3. standard deviation (s)
    4. time between now and the expiration (T – t)

     

    With this spreadsheet you can calculate the upper and lower limit of the strangle with a reliability of 68% and 95%.

    Under alternative formula is a simpler calculation without the use of returns.

     

    If you are interested, I can send you this spreadsheet.

    1 user thanked author for this post.
    avatar Bard
    10/31/2021 at 12:04 PM #180644
    robertogozzi

    Do not include personal information such as email addresses or telephone numbers in your posts.

    You can post any file here as an attachment, if interested.

    Thank you 🙂

     

     

    10/31/2021 at 12:26 PM #180645
    JS

    @robertogozzi where do you see any personal data ???

    10/31/2021 at 12:40 PM #180646
    robertogozzi

    It was a reminder of the widely known rule since you wrote “I can send you“.

    Anything on this forum can be posted  to everyone’s benefit, not sent privately.

     

    10/31/2021 at 12:48 PM #180647
    JS

    In your case with:

    S = 35.805

    Volatility = 17%

    (T – t) = 21

    The 68% interval is between 34061 and 37548

    The 95% interval is between 32318 and 39291

    So you can sell a put option with a strike around 34.000 and sell a call option with a strike around 37.500 (68%)

    Or sell a put option with a strike around 32.300 and sell a call option with a strike around 39.200 (95%)

     

    10/31/2021 at 12:50 PM #180649
    JS

    @robertogozzi I know the rules, thank you 🙂

    10/31/2021 at 3:16 PM #180665
    Bard

    Hi @JS,

    Thank you very much for taking the time to explain the probabilities further, it’s much appreciated!
    This confirms what I have been reading about and of course there’s no need to expand upon the BS model because the standard deviation formula for calculating the future price is given by:
    Price x Volatility x Sq Root (21/365) and multiplying this result by 2 or 3 will give the 2 and 3 standard deviation move amounts and probabilities, (pls see post #180611 above).

    This comment from Quora also gives a little bit more detail about probabilities and option delta values:

    “The rule of thumb is that the Delta of an option approximates the likelihood that the option will expire in-the-money. Since 2 Standard Deviations is the upper and lower bounds of where the stock will close 95% of the time, in only 2.5% of the cases will the stock be below 2 SDs — so the Delta should be in the range of .975 for a call, or -.025 for a put.

    Standard deviation tells us the range of expected future values based on past price history. By definition, 68% of results (in this case, stock prices as of option expiration) will fall within + or – one standard deviation, meaning 32% are expected to fall outside the (+/-) range — 16% above one standard deviation, and 16% below one standard deviation. (btw, I have never seen any research that validates the actual predictive value of standard deviation: I suspect it’s purely theoretical.)

    If you expand the +/- range to two standard deviations, by definition 95% of future events are expected to fall within that range, with 2.5% ending above and 2.5% below the range. Therefore, a call option 2 SDs below strike has a 97.5% chance of expiring in-the-money (ITM) — as of the moment the analysis is done, and holding all other factors equal. (The delta will change as market moves the stock price.) The equivalent put option has a 2.5% likelihood of closing ITM. (Three standard deviations predicts the range that 99.7% of future events should fall within — with a Black Swan being the curve-breaker.)

    The Delta of an option tells us its sensitivity to moves in the underlying stock price — literally how much the market price of an option can be expected to increase should the stock price increase by $1. (For this reason, puts always have negative deltas, since an increase in the stock price should NEVER cause a put’s value to increase.)

    Option deltas are said to approximate the probability that the option will expire in-the-money. An at-the-money call or put has a delta around .5, which means both that it is likely to increase/decrease by 50 cents given a $1 price move — but also that it has a 50% chance of expiring ITM.

    Using this logic, a call two SDs below current ATM strike is deeply ITM, and can be expected to have a delta near 1, given that it has a 97.5% probability of expiring ITM. Actual option price moves are subject to market bid/ask/demand, so the exact move will be more or less than $1.

    A put at the same strike, 2 SDs below market is far OTM, with a 2.5% likelihood of payout at exp. The put delta is likely around -.02 — an expected 2 cent bump if the stock drops a dollar, though this is debatable given that there may be no open interest at that price point, and the Bid/Ask may be negligible. ie: There is no market action that can demonstrate the specificity of the equation.

    A look at some option chains suggests that very close to expiration, the delta is very close to the 2 SD probability, but as expiration gets further away, a 2 SD ITM call will have a delta more in the range of .80 to .90, and puts -.10 to -.20. So much for “Rules of thumb.”

    https://www.quora.com/What-is-the-delta-of-a-2-standard-deviation-below-the-strike-price

    Naturally markets don’t follow a normal distribution and under account for tail risk Black Swan events.

    Thanks once again for your help.

    10/31/2021 at 3:17 PM #180666
    Bard

    Hi @JS,

    That would be great if you could post the Excel sheet?

    Cheers,
    Bard

    10/31/2021 at 4:12 PM #180679
    JS

    Hi @Bard,

    Gladly done, it was a bit of digging into my memory because I have not done anything with options for a while. Long story but also interesting for me to dive in again.

    Forget the Excel sheet because it is better and easier to use the formula “Price x Volatility x Sq. Root (21/365)”.

    Cheers JS

  • Author
    Posts
Viewing 15 posts - 1 through 15 (of 52 total)
1 2 3 4

Find exclusive trading pro-tools on ProRealCode Marketplace

Similar topics:
can you add compounding to a strategy?
having a list of (xls, txt) of all the equity options that offer prorealtime?
how to add voice alert to a code?
how to manual add a line break
pls help on open interest strategies w.r.t us tech 100, dax futures and options

Create your free account now and post your request to benefit from the help of the community
Register or Login