REGRESION & STATISTICAL BANDS
Ver. 2.00 (Log-Normal) by @Xel_Arjona
CHANGES:
- This version could be treated not so much as an update but rather an election over 1.00.a given that the Array field (y axis or price) now is computed as in Logiarithmic scale to catch better moves over penny prices. If you’r an statistical puritan that like to compute deviations and errors over “Normal Distribution” and only use Log-normal calculation’s for returns, you could still use 1.00.a.
- Raw Linear Regression has been supplanted with Time Series Forecast (TSF), which only adds the slope factor to the LinearRegression EndPoint (curve).
Intro:
This is an approach to get in one single indicator one of the best of both mathematical worlds:
From within the STATISTICAL side, everybody well konwn the wide use of the Standard Deviation with a Multiplier Factor from within a Rolling Back MEDIAN (Simple Moving Average) best known as the famous and widly used “Bollinger Band”.
From within the REGRESSION ANALYSIS side, the relevant importance of the STANDARD ERROR with a Multiplier Factor from within an OrdinaryLeastSquares curve generated from the last rolling back sample of the series. For this purpose, a well documented indicator has been posted.
Both indicators are in sync from a uniquie Rolling Back Period window. At this approach, the Regression Analysis tend to “catch” faster moves and volatility while the Statistical band is perfect for mid to long term move confirmation.
Feel free to improve this indicator at www.prorealcode.com.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
// REGRESSION & STATISTICAL BANDS (Log-Normal) AR = LOG(close) N = barindex TSF = linearregression[P](AR) + linearregressionslope[P](AR) M = Average[P](AR) MP = EXP(M) TSFP = EXP(TSF) // BETA bv1 = summation[P](N*AR) - (P*Average[P](N)*Average[P](AR)) bv2 = summation[P](square(N)) - (P*square(Average[P](N))) CalcB = bv1/bv2 // ALPHA CalcA = Average[P](AR) - (CalcB*Average[P](N)) // STANDARD ERROR OF THE ESTIMATE sev1 = Summation[P](square(AR)) - (CalcA*Summation[P](AR)) - (CalcB*Summation[P](N*AR)) sev2 = P - 2 SEE = sqrt(sev1/sev2) // BANDS SeUB = EXP(TSF + (SEE*MF)) SeBB = EXP(TSF - (SEE*MF)) BoUB = EXP(M + (STD[P](AR)*MF)) BoBB = EXP(M - (STD[P](AR)*MF)) // OUTPUT RETURN MP AS "Rollback Median", BoUB AS "+StdDev", BoBB AS "-StdDev", TSFP AS "LinReg Curve", SeUB AS "+SEE", SeBB AS "-SEE" |
Cheers!
Share this
No information on this site is investment advice or a solicitation to buy or sell any financial instrument. Past performance is not indicative of future results. Trading may expose you to risk of loss greater than your deposits and is only suitable for experienced investors who have sufficient financial means to bear such risk.
ProRealTime ITF files and other attachments :PRC is also on YouTube, subscribe to our channel for exclusive content and tutorials
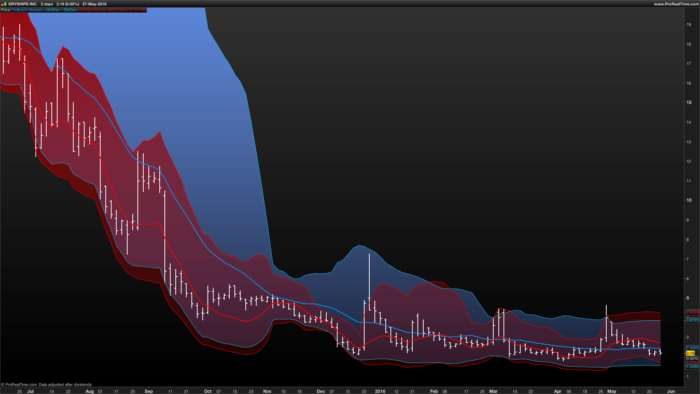

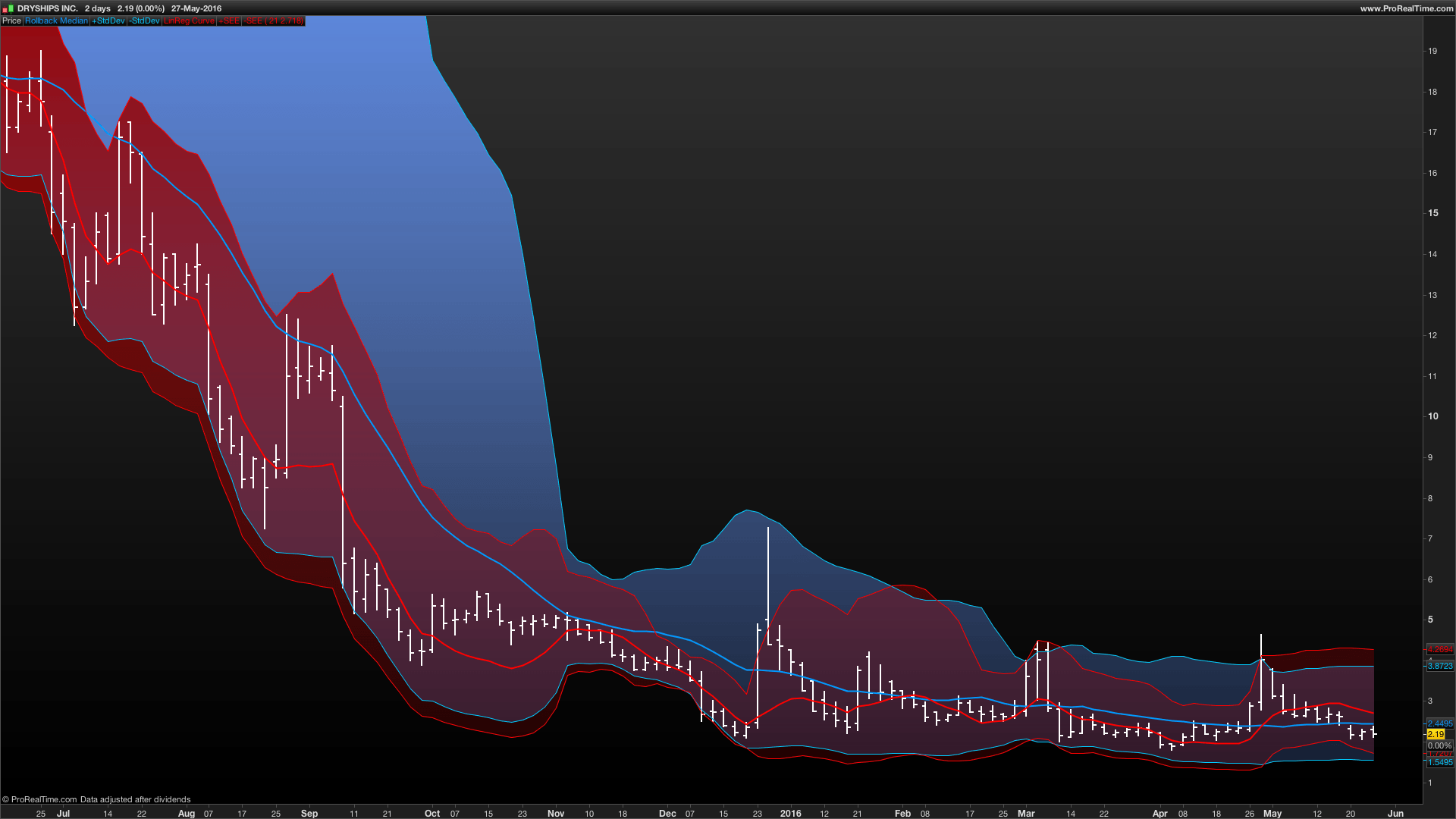
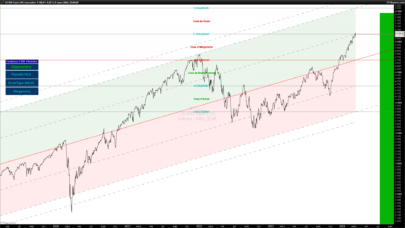
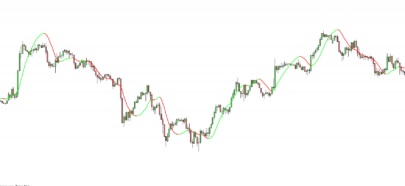
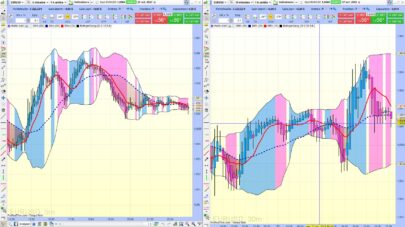
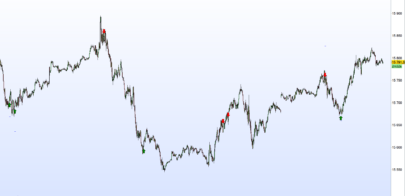
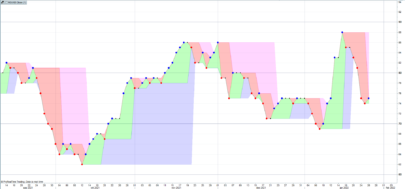
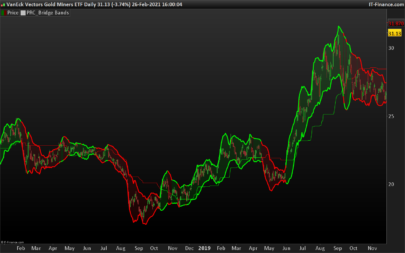
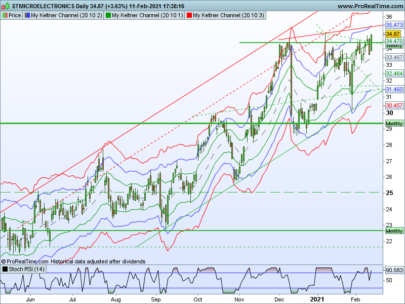
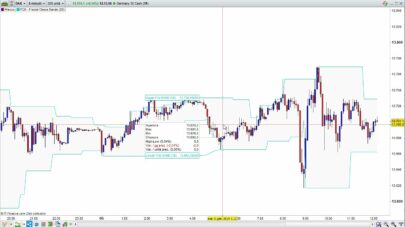
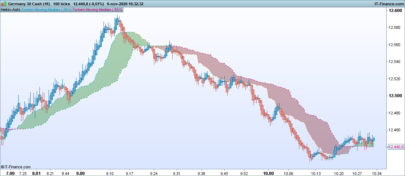
Hi xel and thanks again for posting this kind of nice contribution to the library. I guess you knew what you got in mind while developing this indicator. Maybe you could develop you analysis with everyone here or in a forum post. It would be a great extension of this post with a clean explanation of how to interpret and to use this beauty. Thank you again.
Because the author did not respond and the indicator is one I really liked for doing some research, here is a explanation from another website: https://www.forexrealm.com/technical-analysis/technical-indicators/standard-error-bands.html
My rough interpretation:
If bb is wide and error band is tight, we might have had a strong move.
If bb are tight and error band is wide, we are in sideway’s.
Right?
EXCELENTE INDICADOR,
LOGRÉ CREAR UN SISTEMA QUE ME DA 77 ENTRADAS CON 100% DE EXITO
@DerPat – I don’t see any question regarding the indicator. Anyway, I think I give enough links and explanation how they “work” here and in V1 of the same indicator which do not use logarithmic reading to favor “cent” charts. The math approach for both of them try to weight “volatility” with different algorithm’s in a time-frame static window, one with Standard deviation principle, the other with Standard Error of the Estimate. Deviation tend to “confirm” volatility in a slow pace in contrast with the Standard Error, which act’s fastest (and narrower) than the former one.
Cheers!
Xel, tu eres el creador de este indicador?
Bueno te cuento que es muy bueno para hacer estrategias, en este momento estoy probando una de compra y venta en el par GBP/NZD : 146 ENTRADAS . 5 PERDEDORAS Y 140 GANADORAS , % GANADORAS 95, RATIO GAN/PERD 16.67, NO PRODUCE SEÑALES FALSAS DURANTE 3 MESES EN 10 MINUTOS-
ESO SI, NO UTILIZO UNICAMENTE ESTE INDICADOR , UTILIZO OTRO DE ESTA MISMA PAGINA , TAMBIEN MUY , PERO MUY BUENO.
SI LAS PRUEBAS EN CUENTA REAL ME SALEN POSITIVAS , TE LO MANDO. HASTA AHORA ME HA ABIERTO 2 POSICIONES GANADORES Y NINGUNA PERDEDORA
Buen día @diegofe_2000 – Claro, mandalo y por aquí lo probamos en otros instrumentos y si gustas, lo portamos a otras plataformas. Saludos.